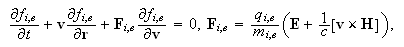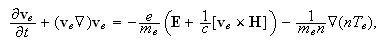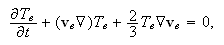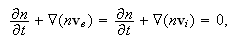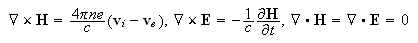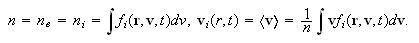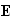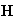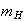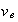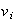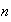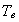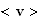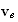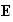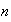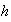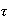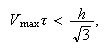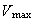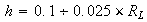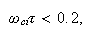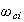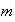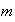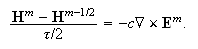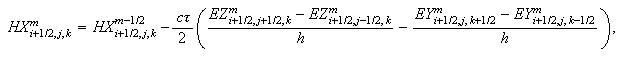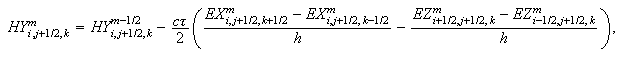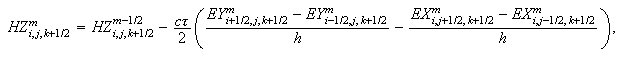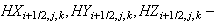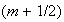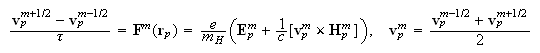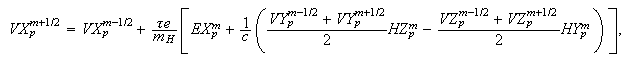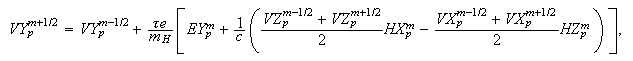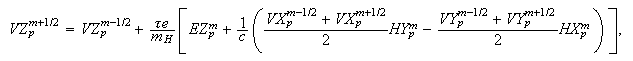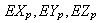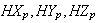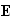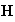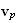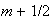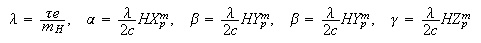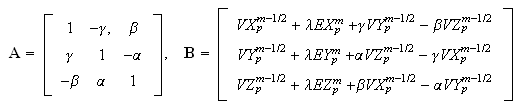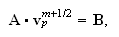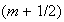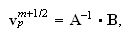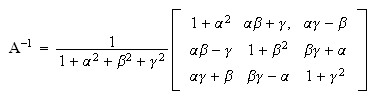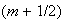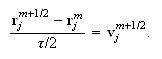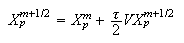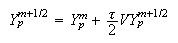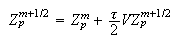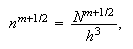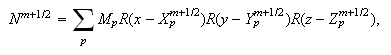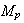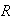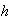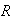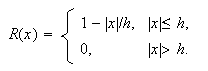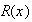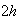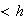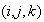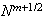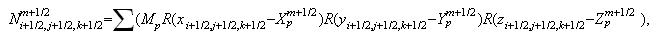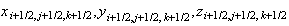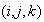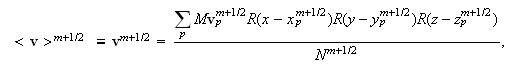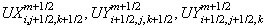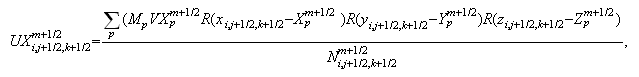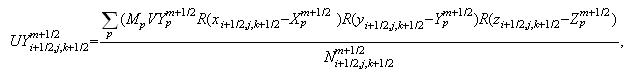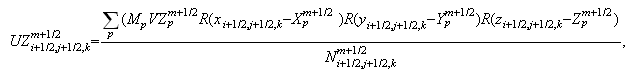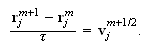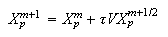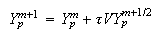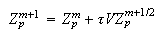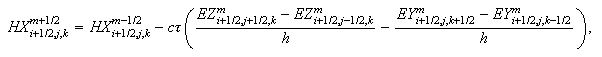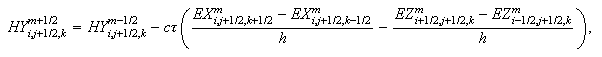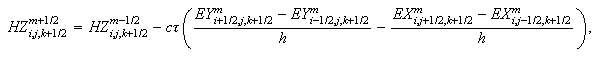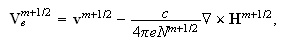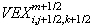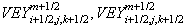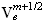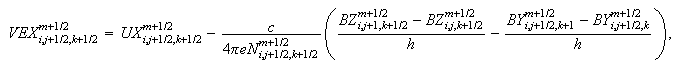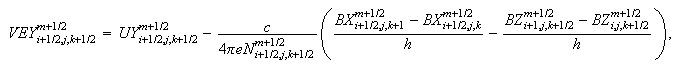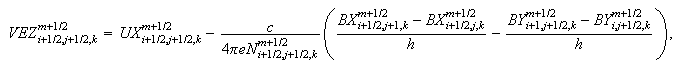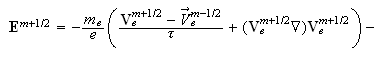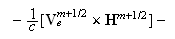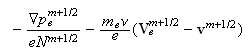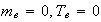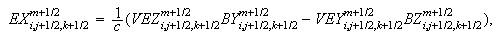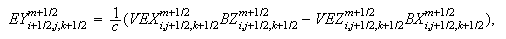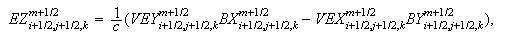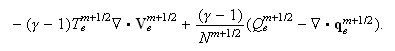Моделирование динамики бесстолкновительной плазмы в OpenPIC3D
Д. А. Осипян
Программа
OpenPIC3D
предназначена
для
моделирования
различных
задач
динамики
бесстолкновительной
плазмы (ДБСП).
OpenPIC3D
реализован
на языке С++,
поддерживает
стандарты
параллельных
вычислений MPI
и OpenMP. Доступны
версии OpenPIC3D для
Unix, Linux и Windows.
Начальные и
граничные
условия
задач ДБСП
задаются с
помощью
интерпретруемого
конфигурационного
скрипта на
языке Lua.
Кинетико-гидродинамическая
модель.
Во многих
задачах ДБСП
ионы плазмы
не являются
замагниченными,
поскольку
ларморовский
радиус
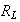 ионов
сравним с
характерными
размерами
физического
явления.
Поэтому для
их описания
необходимо
использовать
кинетические
уравнения.
Для описания
движения
электронов
используется
гидродинамическое
приближение,
так как их
ларморовский
радиус
гораздо
меньше
ларморовского
радиуса
ионов.
Например, в
задаче
торможения
разлетающегося
облака в
фоновой
плазме,
физическим
обоснованием
такой
гибридной
модели
служит тот
факт, что в
результате
торможения
может
генерироваться
бесстолкновительная
ударная
волна (БУВ) с
гидродинамическим
опрокидыванием
переднего
фронта и
образованием
областей
многопотокового
течения.
Поэтому
структура
такой
сверхкритической
БУВ на
пространственных
масштабах
ионов
сравним с
характерными
размерами
физического
явления.
Поэтому для
их описания
необходимо
использовать
кинетические
уравнения.
Для описания
движения
электронов
используется
гидродинамическое
приближение,
так как их
ларморовский
радиус
гораздо
меньше
ларморовского
радиуса
ионов.
Например, в
задаче
торможения
разлетающегося
облака в
фоновой
плазме,
физическим
обоснованием
такой
гибридной
модели
служит тот
факт, что в
результате
торможения
может
генерироваться
бесстолкновительная
ударная
волна (БУВ) с
гидродинамическим
опрокидыванием
переднего
фронта и
образованием
областей
многопотокового
течения.
Поэтому
структура
такой
сверхкритической
БУВ на
пространственных
масштабах
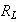 может быть
адекватно
описана
только на
базе
гибридного
приближения.
может быть
адекватно
описана
только на
базе
гибридного
приближения.
Исходная
система
уравнений
для
описанной
кинетико-гидродинамической
(гибридной)
состоит из
кинетичекого
уравнения
Власова для
ионов,
уравнения
движения и
изменения
внутренней
энергии для
электронной
компоненты,
а также
уравнений
Максвелла
для
электромагнитного
поля,
которая в
случае
водородной
плазмы имеет
вид: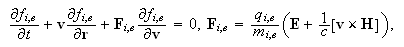
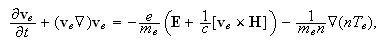
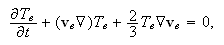
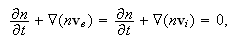
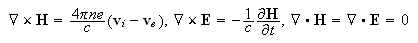
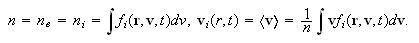 Здесь
Здесь
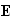 ,
,
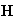 --
напряжённости
электрического
и магнитного
полей,
--
напряжённости
электрического
и магнитного
полей,
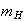 -- масса иона
водорода,
-- масса иона
водорода,
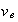 ,
,
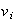 --
среднемассовые
скорости
электронов и
ионов,
--
среднемассовые
скорости
электронов и
ионов,
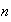 --
концентрация
ионов,
--
концентрация
ионов,
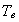 --
температура
электронов.
Заметим, что
в уравнениях
(1) -- (6)
отброшены
все
диссипативные
члены,
связанные с
конечной
проводимостью,
вязкостью и
теплопроводностью
плазмы.
--
температура
электронов.
Заметим, что
в уравнениях
(1) -- (6)
отброшены
все
диссипативные
члены,
связанные с
конечной
проводимостью,
вязкостью и
теплопроводностью
плазмы.
Алгоритм OpenPIC3D
Расчёты
проводятся
на сдвинутых
сетках (рис. 1),
что повышает
точность
решения.
Компоненты
средних
скоростей
частиц
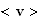 и электронов
и электронов
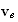 хранятся в
тех же узлах,
что и
компоненты
вектора
хранятся в
тех же узлах,
что и
компоненты
вектора
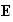 напряжённости
электрического
поля.
Плотность
напряжённости
электрического
поля.
Плотность
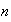 частиц
хранится в
центре
ячейки.
частиц
хранится в
центре
ячейки.
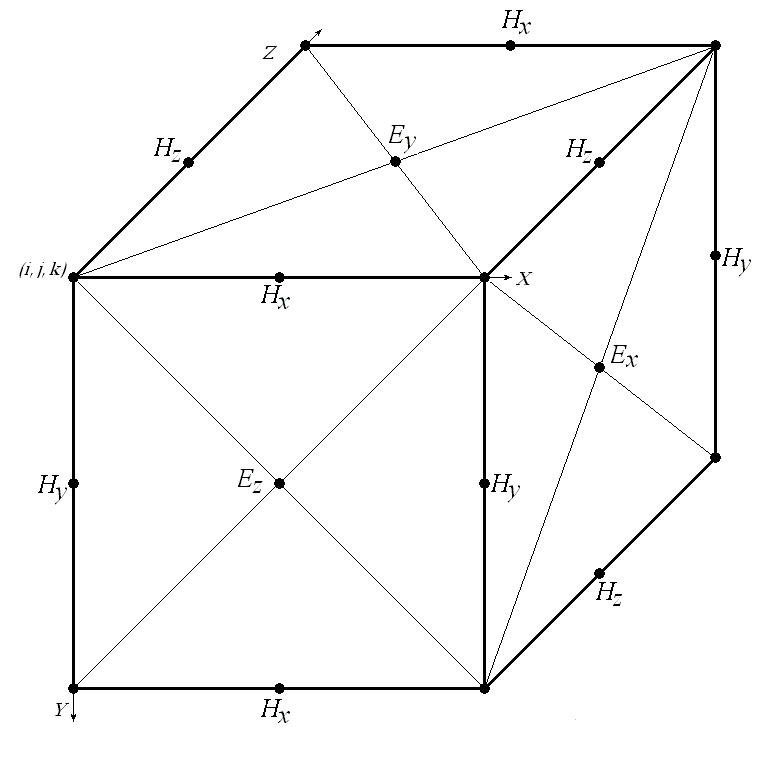
Шаг
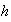 кубической
сетки и шаг
кубической
сетки и шаг
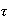 по времени
выбирается в
соответствии
с условием
Куранта-Фридрикса-Леви:
по времени
выбирается в
соответствии
с условием
Куранта-Фридрикса-Леви:
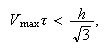 где
где
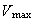 --
максимальная
скорость,
детальностью
моделирования:
--
максимальная
скорость,
детальностью
моделирования:
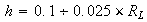 и условия
устойчивости
интегрирования
уравнений
движения:
и условия
устойчивости
интегрирования
уравнений
движения:
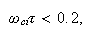 где
где
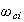 -- ионная
циклотронная
частота.
-- ионная
циклотронная
частота.
Алгоритм
расчёта на
каждом шаге
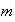 по времени
состоит из
следующих
этапов:
по времени
состоит из
следующих
этапов:
-
Вычисление
предварительного
значения
магнитного
поля
(временнòй
слой
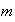 ):
):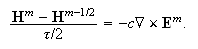
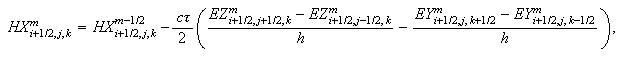
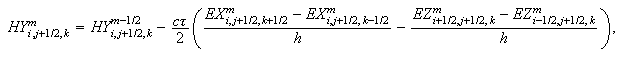
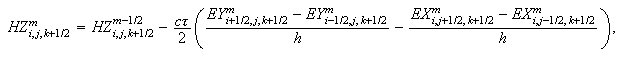
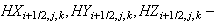 компоненты
вектора
компоненты
вектора
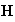 .
.
-
Вычисление
скорости
частиц на
слое
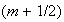 :
: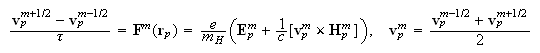
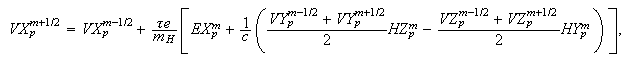
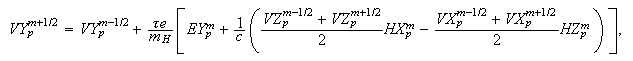
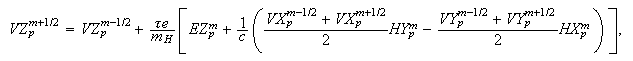
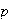 -- номер
(индекс)
частицы,
-- номер
(индекс)
частицы,
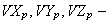 компоненты
вектора
скорости
компоненты
вектора
скорости
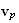 частицы.
частицы.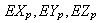 и
и
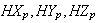 -- компоненты
векторов
-- компоненты
векторов
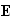 и
и
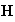 в точке
нахождения
частицы.
Значения
этих
компонент
вычисляются
интерполяцией
по значениям
ближайших к
частице
восьми узлов
пространственной
сетки.
Приведенная
система
линейных
алгебраических
уравнений
для
компонент
скорости
в точке
нахождения
частицы.
Значения
этих
компонент
вычисляются
интерполяцией
по значениям
ближайших к
частице
восьми узлов
пространственной
сетки.
Приведенная
система
линейных
алгебраических
уравнений
для
компонент
скорости
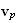 частицы
на слое
частицы
на слое
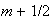 решается
аналитически.
Введём
сдедующие
обозначения:
решается
аналитически.
Введём
сдедующие
обозначения:
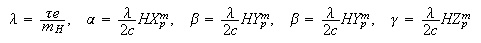
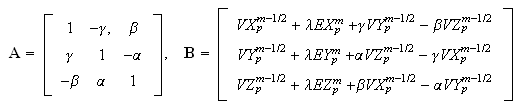 тогда
система (8)
может быть
представлена
в матричной
форме:
тогда
система (8)
может быть
представлена
в матричной
форме: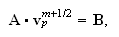
и скорости
частиц на
слое
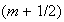 могут быть
вычислены по
формуле:
могут быть
вычислены по
формуле: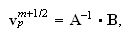
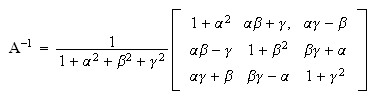
-
Координаты
частиц на
слое
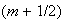 :
: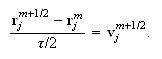
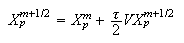
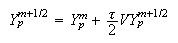
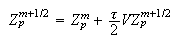 Плотности
заряда
частиц:
Плотности
заряда
частиц: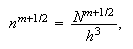
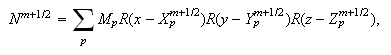 где
где
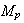 -- заряды
отдельных
частиц,
-- заряды
отдельных
частиц,
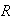 -- ядро
PIC-метода. Для
равномерной
сетки с
шагом
-- ядро
PIC-метода. Для
равномерной
сетки с
шагом
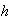 ядро
ядро
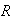 имеет
вид:
имеет
вид: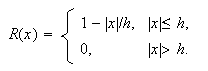
Функция
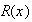 отлична от
нуля только
на интервале
длиной
отлична от
нуля только
на интервале
длиной
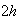 ,
поэтому
суммирование
в (9)
производится
по частицам,
находящимся
на
расстоянии
,
поэтому
суммирование
в (9)
производится
по частицам,
находящимся
на
расстоянии
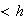 от узла
ячейки. Т.к.
плотности
зарядов
частиц
хранятся в
центрах
ячеек, то для
ячейки с
индексом
от узла
ячейки. Т.к.
плотности
зарядов
частиц
хранятся в
центрах
ячеек, то для
ячейки с
индексом
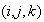 расчёт
расчёт
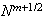 проводится
по
формуле:
проводится
по
формуле: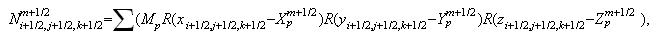 Здесь
Здесь
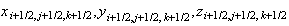 --
координаты
центра
ячейки с
индексом
--
координаты
центра
ячейки с
индексом
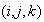
-
Cредние
скорости
частиц: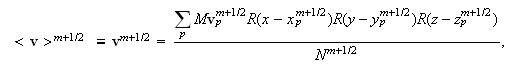 Для
компонент
Для
компонент
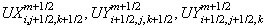 вектора
средней
скорости
вектора
средней
скорости
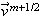 частиц
получаем:
частиц
получаем: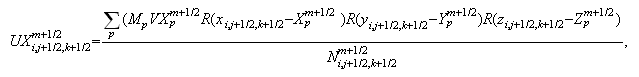
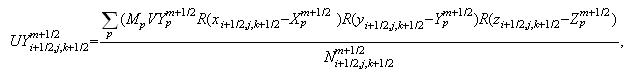
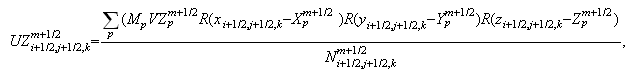
-
Координаты
частиц и
плотность
заряда на
слое
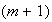 :
: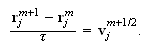
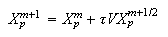
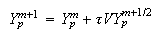
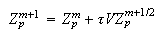
-
Окончательное
значение
магнитного
поля: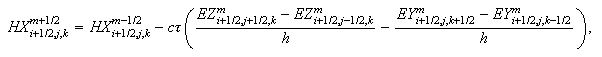
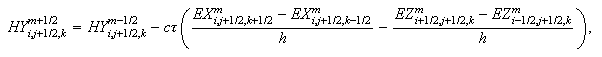
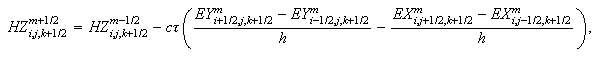
-
Вычисление
скорости
электронов: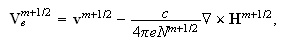
Для
компонент
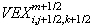 ,
,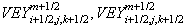 вектора
скорости
вектора
скорости
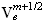 электронов
получаем:
электронов
получаем:
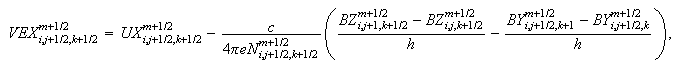
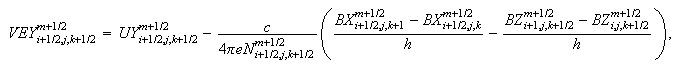
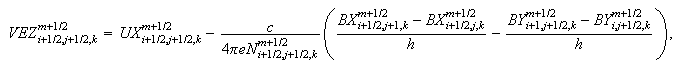
-
Вычисление
электрического
поля:
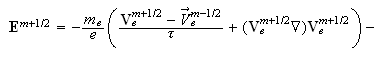
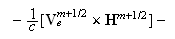
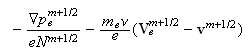
Для случая
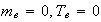 (обоснованность
этого
предположения
см. в
ссылках):
(обоснованность
этого
предположения
см. в
ссылках):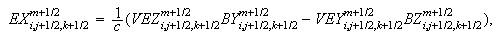
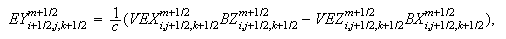
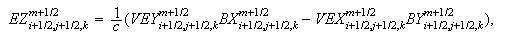
Здесь
компоненты
магнитного
поля
находятся
как
среднеарифметические
двух
соседних
узлов, а
компоненты
скорости
электронов --
как
среднеарифметические
четырёх
соседних
узлов.
-
Вычисление
температуры
электронов
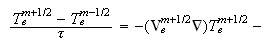
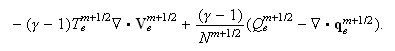
Объекты OpenPIC3D
OpenPIC3D
представляет
собой
вычислительный
модуль
описанной
выше
гибридной
модели,
который
реализован в
исполняемом
файле opic3d (в *nix)
или opic3d.exe (в Windows).
Для описания
вычислительной
задачи
используется
конфигурационный
Lua-скрипт,
задаваемый в
качестве
аргумента
командной
строки.
Например,
с:\OpenPIC3D>opic3d.exe solarwind.lua
запускает
программу
opic3d.exe и
передаёт ей
в качестве
аргумента
конфигурационный
скрипт solarwind.lua
с описанием
начальных и
граничных
условий
конкретной
задачи.
Вычислительный
модуль (opic3d.exe)
экспортирует
в скрипт
следующие
объекты,
необходимые
для
установки
начальных и
граничных
условий
задачи и
параметров
расчёта:
-
pic_grid
-
--
объект типа
Grid --
расчётня
сетка;
-
pic_particles
-
--
объект типа
Particles --
набор модельных
частиц;
-
pic_particle_groups
-
--
объект типа
ParticleGroups -- группы
частиц;
-
pic_marker_particles
-
--
объект типа
MarkerParticles --
индексы
маркированных
частиц;
-
pic_parameters
-
--
объект типа
Parameters -- общие
параметры
расчёта;
-
pic_grid_save_filters
-
--
объект типа
GridSaveFilters --
набор пользовательских
фильтрв для
записи
сеточных
значений;
Типы
объектов OpenPIC3D,
их методы и свойства
-
Parameters --
представляет
общие
параметры
расчёта.
-
double tau
-
--
временнòй
шаг расчёта;
-
size_t time_steps
-
--
количество
шагов по
времени;
-
size_t current_time_step
-
--
номер
текущего
шага по
времени (readonly);
-
size save_time_steps
-
--
период
сохранения
данных на
диске (readonly);
-
double dens_cutoff
-
--
минимальная
допустимая
концентрация
частиц в
ячейке;
-
bool save_all_particles
-
--
флаг
сохранения
всех частиц;
-
bool save_whole_grid
-
--
флаг
сохранения
всей сетки;
-
bool save_grid_x_plains
-
--
флаг
сохранения
всех
плоскостей:
x = k*pic_grid.step, k = 0..pic_grid.size_x-1;
-
bool save_grid_y_plains
-
--
флаг
сохранения
всех
плоскостей:
y = k*pic_grid.step, k = 0..pic_grid.size_y - 1;
-
bool save_grid_z_plains
-
-- флаг
сохранения
всех
плоскостей:
z = k*pic_grid.step, k = 0..pic_grid.size_z - 1;
-
process_idx
-
--
индекс
текущего
процесса,
используется
в MPI (readonly).
-
DblVector -
трёхмерный
вектор.
-
double x , y, z
-
--
компоненты
вектора;
-
DblVector()
-
--
конструктор
по
умолчанию.
-
DblVector(const DblVector& other)
-
--
конструктор
копирования;
-
DblVector(double x , double y, double z )
-
--
перегруженный
конструктор.
-
double abs()
-
--
возвращает
модуль
вектора.
-
Cell -- ячейка
расчётной
сетки.
-
double Bx, By,Bz
-
--
компоненты
напряжённости
магнитного
поля;
-
double Ex, Ey, Ez
-
--
компоненты
напряжённости
электрического
поля;
-
doubleUEx, UEy, UEz
-
--
компоненты
электронной
скорости;
-
double UPx, UPy, UPz
-
--
компоненты
ионной
скорости;
-
double NP
-
--
концентрация
ионов;
-
bool active
-
--
флаг
активности
ячейки;
-
Cell()
-
--
конструктор
по
умолчанию.
-
Cell(const Cell& other)
-
--
конструктор
копирования;
-
Cell(double NP,
-
const
DblVector& vec_B, const DblVector& vec_E,
-
const
DblVector& vec_UE, const DblVector& vec_UP)
-
--
перегруженный
конструктор.
-
Grid --
расчётная
сетка.
-
size_t size_x, size_y, size_z
-
--
количество
узлов сетки
по осям x, y, z;
-
double length_x, length_y, length_z
-
--
размеры
расчётной
области по
осям x, y, z;
-
double step
-
--
шаг сетки.
-
Cell& at(size_t x, size_t y, size_t z)
-
--
возвращает
ссылку на
ячейку с
индексом (x, y,
z).
-
void resize(size_t sx, size_t sy, size_t sz)
-
--
устанавливает
количество
узлов сетки
по осям x, y, z;
-
void set(size_t x, size_t y, size_t z, const Cell& cell)
-
--
присваивает
значение node
ячейке индексом
(x, y, z).
-
GridSaveFilters --
представляет пользовательские
фильтры для
записи
сеточных
значений
-
void add(const string& filter_name)
-
--
добавляет
фильтр с
именем filter_name.
-
filter_name
-
--
имя функции
в
конфигурационном
скрипте, которой
при каждом
сохранении
данных
-
будут
передаваться
координаты
очередной
точки.
-
Если
результат
вызова равен
true, то
сеточные
значения в
точке будут
записаны
-
в
файл filter_name_grd_S.dat(S -
номер
шага).
-
Пример:
-
function diagonal_points(x, y, z)
-
return (x == y and y == z)
-
end
-
.
. .
-
pic_grid_save_filters:add("diagonal_points")
-
-
Во
время
расчёта в
файл diagonal_points_grd_S.dat
-
будут
записаны
сеточные
значения в
точках,
координаты
которого
-
удовлеворяют
условию,
указанному в
функции
-
diagonal_points(x,
y, z);
-
Particle --
представляет
модельную
частицу
(макрочастицу).
-
group_name
-
--
имя группы
частиц,
которой
принадлежит
данная
частица;
-
double ni
-
--
количество
ионов,
представляемых
данной
частицей;
-
double x, y, z
-
--
координаты
частицы;
-
double v_x, v_y, v_z
-
--
компоненты
скорости
частицы;
-
Particle()
-
--
конструктор
по
умолчанию.
-
Particle(const Particle& other)
-
--
конструктор
копирования;
-
Particle(const string& group_name,
-
const
DblVector& vec_r,
-
const
DblVector& vec_v,
-
double
ni)
-
--
перегруженный
конструктор.
-
Particle(const string& group_name,
-
double
x, double y, double z,
-
double
v_x, double v_y, double v_z,
-
double
ni)
-
--
перегруженный
конструктор.
-
Particles --
представляет
массив
модельных
частиц.
-
size_t size
-
--
количество
частиц.
-
Particles()
-
--
конструктор
по
умолчанию.
Создаёт
пустой
массив
модельных
частиц;
-
Particle& at(size_t i)
-
--
возвращает
ссылку на
частицу с
индексом i;
-
void set(size_t i, const string& group_name, const Particle&
p)
-
--
i - й частице
присваивает
значение p;
-
void set(size_t i, const string& group_name,
-
const
DblVector& vec_r, const DblVector& vec_v, double ni)
-
--
свойствам
частицы c
индексом i
присваиваются
переданные
значения;
-
void add(const Particle& p)
-
--
добавляет
частицу p в
конец
массива;
-
void add(const string& group_name, const
DblVector& vec_r,
const
DblVector& vec_v, double ni)
-
--
создаёт
частицу с
указанными
свойствами и
добавляет её
в конец
массива;
-
void erase(size_t i)
-
--
удаляет
частицу c
индексом i.
-
ParticleGroups --
представляет
группы
частиц
-
bool create_group(const string& name, double charge, double
mass, Diag diag)
--
создаёт
группу
частиц с
именем name,
зарядом
ионов charge (в
единицах
заряда
протона),
массой
ионов mass (в
единицах
массы
протона).
-
MarkerParticles --
представляет
набор
маркированных
частиц
-
void add(size_t i)
-
--
добавляет
частицу c
идексом i.
Литература
-
Малышкин В.,
Вшивков В.,
Краева М. О
реализации
метода
частиц на
мультипроцессорах.
Новосибирск,
1995.
-
Григорьев
Ю.Н., Вшивков
В.А.
"Численные
методы
"частицы - в -
ячейках".
Новосибирск,
Наука,
Сибирская
издательская
фирма РАН, 2000.
-
Р. Хокни, Дж.
Иствуд.
Численное
моделирование
методом
частиц. Мир, М.,
1987.
-
Ч. Бэдсел, А.
Ленгдон.
Физика
плазмы и
численное
моделирование.
Энергоатомиздат,
М., 1989.
-
H. Matsumoto and Y. Omura. Computer Space Plasma Physics: Simulation
Techniques and Software. Radio Atmospheric Science Center, Kyoto University,
Kyoto, Japan. 1993.
-
J. Buchner, M. Scholer, C. T. Dum. Space plasma simulation. Springer,
2003.
 ионов
сравним с
характерными
размерами
физического
явления.
Поэтому для
их описания
необходимо
использовать
кинетические
уравнения.
Для описания
движения
электронов
используется
гидродинамическое
приближение,
так как их
ларморовский
радиус
гораздо
меньше
ларморовского
радиуса
ионов.
Например, в
задаче
торможения
разлетающегося
облака в
фоновой
плазме,
физическим
обоснованием
такой
гибридной
модели
служит тот
факт, что в
результате
торможения
может
генерироваться
бесстолкновительная
ударная
волна (БУВ) с
гидродинамическим
опрокидыванием
переднего
фронта и
образованием
областей
многопотокового
течения.
Поэтому
структура
такой
сверхкритической
БУВ на
пространственных
масштабах
ионов
сравним с
характерными
размерами
физического
явления.
Поэтому для
их описания
необходимо
использовать
кинетические
уравнения.
Для описания
движения
электронов
используется
гидродинамическое
приближение,
так как их
ларморовский
радиус
гораздо
меньше
ларморовского
радиуса
ионов.
Например, в
задаче
торможения
разлетающегося
облака в
фоновой
плазме,
физическим
обоснованием
такой
гибридной
модели
служит тот
факт, что в
результате
торможения
может
генерироваться
бесстолкновительная
ударная
волна (БУВ) с
гидродинамическим
опрокидыванием
переднего
фронта и
образованием
областей
многопотокового
течения.
Поэтому
структура
такой
сверхкритической
БУВ на
пространственных
масштабах
 может быть
адекватно
описана
только на
базе
гибридного
приближения.
может быть
адекватно
описана
только на
базе
гибридного
приближения.